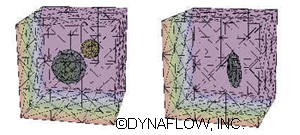
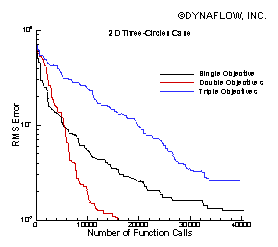
2DynaEIT© is a suite of efficient and accurate algorithms for solution of the two-dimensional forward and inverse Electrical Impedance Tomography (EIT) problems. The forward problem is the problem of determination of voltage and current distribution for known conductivity distribution in the imaged domain, while the inverse problem is the problem of image reconstruction using the measured voltages and/or currents.

The forward problem consists in solving the Laplace equation for the electrical potential. The software applies the highly efficient Boundary Element Method (BEM) for the numerical solution and the user can use the forward solver to provide data similar to that obtained experimentally.

In the inverse problem, the distribution of conductivity inside a container is sought by applying specified voltages at the electrodes located on the container surface, and performing measurements of the currents at the same locations. For two-phase flows, 2DynaEIT© assumes that the domain to be imaged consists of regions of zero conductivity, i.e. cavities embedded in a continuous phase of another material of almost constant conductivity, e.g. bubbles in a liquid and cracks in a structure. Therefore, the map of conductivity distribution is represented directly by the material interfaces inside the domain.

To reduce the CPU time a Dipole approximation method is also implemented in 2DynaEIT©. The converged Dipole approximation solution can be used as an initial “guess solution” for the full BEM.

In 2DynaEIT© the minimization techniques include a gradient based scheme, a Powell Direction Set Method, and an evolutionary optimization scheme, Genetic Algorithm (GA). A combination of both the Powell Method and GA allows the inverse computation to reach a global minimum much.

The software uses a Graphical User Interface to facilitate input of the internal cavity shapes for the forward problem as well as input of optimization parameters for the inverse problem. 2DynaEIT© is the 3D equivalent to 2DynaEIT© and is available as a console version.

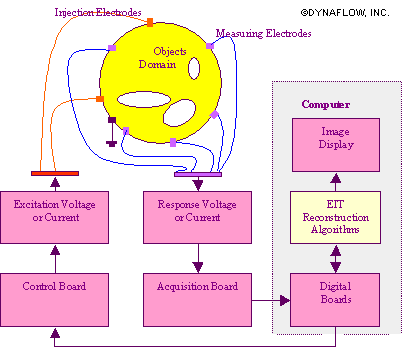
Principle:

In Electrical Impedance Tomography (EIT) the distribution of impedance inside a container is sought by applying specified currents (or voltages) at some parts of the container surface, and performing measurements of the voltage (or current) at some other parts. The equations for the electric field then provide relationships between the conductivity distribution inside the domain and the measured voltages and currents. Different types of materials have different conductivities, and the availability of a conductivity map provides an image of the material distribution in the container. The initial efforts to develop the technology were funded by Small Business Innovation Research (SBIR) awards from the National Science Foundation.  

 
Schematic of the Electrical Impedance Tomography Method.
 

Reconstructed objects in a cubical domain using Genetic Algorithmand Singular BEM: 2 spheres (8 parameters) and an ellipsoid (9 parameters). Converged solutions are on top of the exact solution.
Reconstructed arbitrary objects in a cylindrical domain using a Boundary Element Method and  approximation with 3 location and 4 shape parameters for each object (on the right) and 32 parameter point parameterization for star-like object (on the left).
 

Applications:

The two and three-dimensional EIT algorithms can be applied for medical imaging, multiphase flows imaging  encountered in chemical, oil and gas, energy, and aerospace industries, non-destructive evaluation of structures and materials, imaging of underground water paths and container leakage, archaeology, detection of buried objects, chemical reactive flows, and many others. 

Application areas of EIT software are not limited by imaging based on electrical properties since the methods of solution are based on the solution of the classical Laplace, Poisson, and Helmholtz equations which describe a wide variety of physical phenomena. These include filtration, acoustical, optical, thermal, and other processes. The developed software can be adjusted for such problems as evaluation of oil and gas deposits, based on log data, seismic imaging, and imaging of temperature and pressure fields in various industries.
Comparison of convergence histories for reconstruction of 3 circles using Boundary Element Method, Genetic Algorithm, and single-, double-, and triple- objective minimization.
 
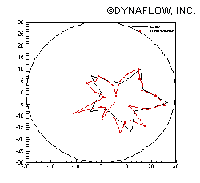
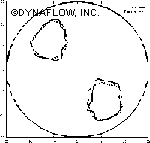
Reconstructed objects in a cylindrical domain using Dipole Approximation and Powell's Direction Set Method (on the left). The number of objects is 2 (red). The number of dipoles used for reconstruction is 5 (black). The graph on the right shows voltages on electrodes for correct and converged solutions.